Modifier le centrage d'un avion
08 nov. 2013J'ai parlé dans d'autres articles des test de centrage d'un avion ou d'un planeur. Ok, mais si le centrage n'est pas bon comment faire pour le modifier ? De même si lorsque on a terminé son nouvel avion on se rend compte que le centrage n'est pas au bon endroit (par rapport au plan, ou à PredimRC par exemple).
Deux solutions sont envisageables pour modifier le centrage : soit déplacer des éléments se trouvant dans l'avion (pack d'accus en propulsion électrique), soit ajouter un lest. la première solution est bien entendu la meilleure car elle n'augmente pas la masse de l'avion, mais encore faut-il pouvoir l'appliquer. Dans des cas extrèmes on cumulera les deux solutions (par exemple si le centre de gravité est trop arrière : avancer tout ce qui peut l'être et ajouter du lest).
En ce qui concerne le déplacement d'un élément, son effet peut être calculé par une formule très simple :
- si la masse de l'avion est M
- la masse de l'élément que l'on bouge est m
- on déplace l'élément en question de x centimètres (x positif si on le déplace vers l'avant, négatif si c'est vers l'arrière)
alors le CG bouge de x * m / M
(le CG recule si on a déplacé la masse m vers l'arrière et avance si on l'a déplacée vers l'avant).
En relisant cet article je me suis dit "tiens, c'est bizarre, la formule ne prends pas en compte la position initiale de la masse m". J'ai trouvé cela contre-intuitif alors pour ceux qui se poseraient la même question j'ai repris le calcul que je détaille ci dessous.
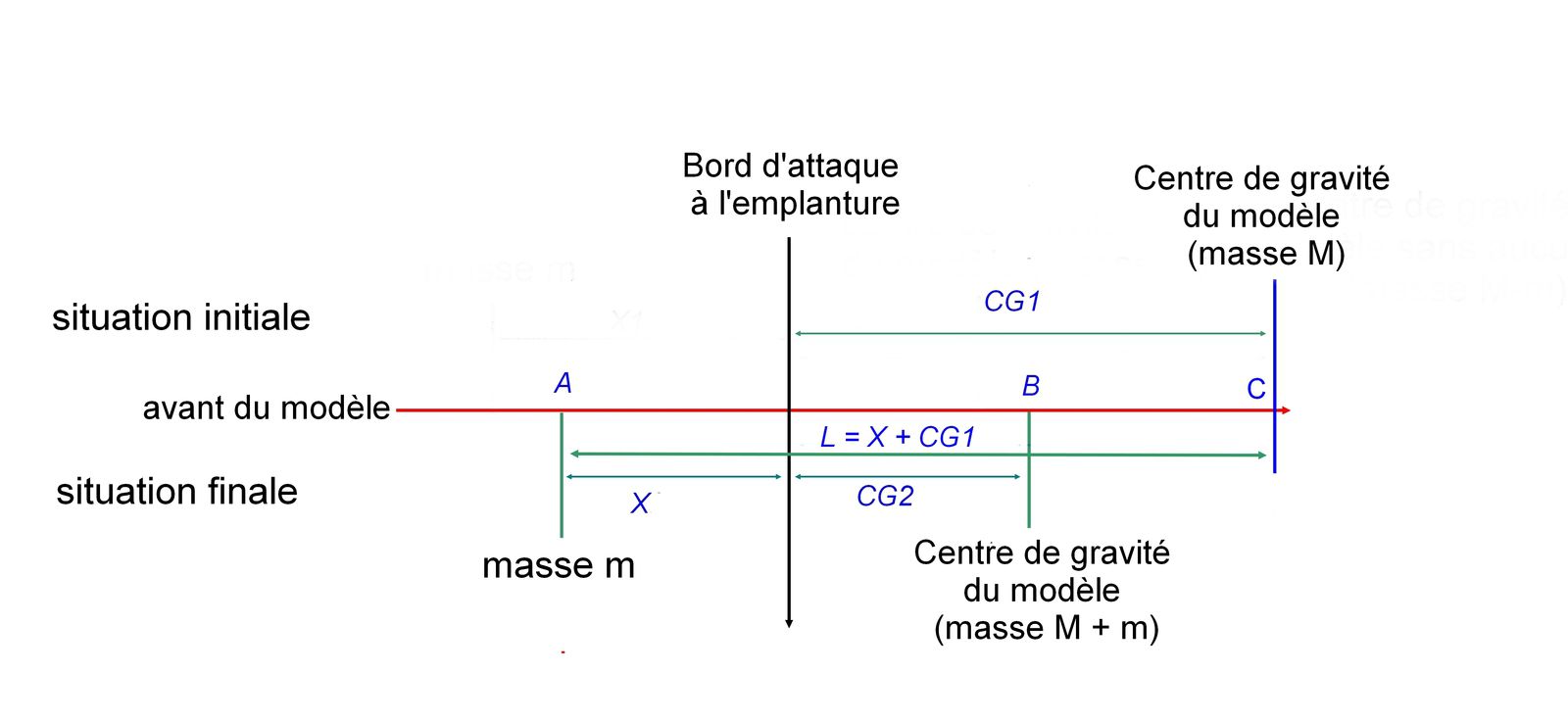
D'abord un petit dessin (oui, je sais, je n'ai pas fait trop d'efforts le dessin est sommaire ...) pour mieux visualiser la situation et définir les variables :
Et maintenant le calcul. Je peux écrire deux équations correspondant la première à la situation initiale, et la seconde à la situation finale :
(X1+CG1) * m = (L - CG1) * (M - m) (1)
(X2+CG2) * m = (L - CG2) * (M - m) (2)
Je soustrait les deux équations et j'obtiens :
((X1+CG1) - (X2+CG2) ) * m = ((L - CG1) - (L - CG2)) * (M - m)
Et en secouant un peu :
(X1 - X2) * m + (CG1 - CG2) * m = - (CG1 - CG2) * M + (CG1 - CG2) * m
d'ou
(X1 - X2) * m = - (CG1 - CG2) * M et donc : CG1 - CG2 = - (m/M) * (X1 - X2).
Le signe "-" peut dérouter. Il traduit tout simplement le fait que si X1 est plus grand que X2 (la masse est déplacée vers l'arrière du modèle) la distance du centre de gravité à l'emplanture augmente (le centre de gravité recule).
Par exemple, sur un modèle de 2kg400 en ordre de bol (avec son pack) :
- j'avance de 5 cm mon pack d'accus de 400 grammes, le CG avance de 8,3 mm
- j'avance de 10 cm mon récepteur qui pèse 20 grammes, le cg avance de moins de 1 mm
on voit pourquoi sur un modèle thermique il n'y a pas grand chose à gagner. Et aussi pourquoi on a intérêt à bien attacher le pack dans le fuselage pour qu'il ne bouge pas. Je me souviens d'un vol avec le Monsun ou le pack avait glissé en position arrière (oubli de la mousse de maintien), reculant de quelques centimètres, l'appareil était devenu très désagréable en vol et délicat à piloter et je m'étais posé en urgence.
Deuxième solution, si on ne peut pas modifier l'emplacement du pack de réception, il faut ajouter du poids. A l'avant de l'appareil si on veut avancer le centre de gravité, à l'arrière si on veut le reculer. Là aussi on peut calculer la variation de centre de gravité en sachant quelle masse on ajoute, et où on la positionne. Mais dans ce cas la compréhension du résultat est un peu plus compliquée pour des questions de signe des variables (nous parlons toujours en valeur absolue en utilisant les termes "en avant de" et "en arrière de" pour dire ou se situe précisément le lest, le centre de gravité ,etc : le lest est 20 cm en avant de l'emplanture, le cg est 10 cm en arrière de l'emplanture, ...), de point par rapport auquel on mesure les distances et de conventions modélistes (le Cg est situé par rapport à l'emplanture).
Donc je préfère décomposer en 2 formules, selon que la masse est située devant ou derrière le centre de gravité. Les hypothèses communes sont : la masse de l'avion est M, la masse de l'élément que l'on ajoute est m et le centre de gravité initial se situe à CG1 cm de l'emplanture (CG1 positif si situé derrière l'emplanture ce qui est généralement le cas))
1er cas : la masse est ajoutée à L cm en avant du centre de gravité :
Alors le CG avance de L * ( m ) / ( M + m ) .
2ème cas : la masse est ajoutée à L cm en arrière du centre de gravité :
Alors le CG recule de L * ( m ) / ( M + m ) .
L est dans les deux cas positifs.
Je vois un élève de premier rang qui réclame la démonstration mathématique. Ok ... Avec d'abord un petit croquis pour repérer les variables. Et je ne vais traiter et expliquer que le premier cas (la masse est en avant du centre de gravité)
Ici, on se contente d'écrire une seule équation, correspondant à la situation finale. Cette équation traduit l'égalité des moments des deux forces s'appliquant au modèle (due à masse m en A et masse M en C) par rapport au centre de gravité :
(X + CG2) * m = (CG1 - CG2) * M
Telle qu'est l'équation je ne vais pas arriver à faire apparaître une relation ou apparaît la variation de position du centre de gravité. Donc je ré-écrit la formule en remplaçant à gauche CG2 par CG2 - CG1 + CG1 . Il vient :
(X + CG2 - CG1 + CG1) * m = (CG1 - CG2) * M
d'ou : (X + CG1) * m + (CG2 - CG1) * m = (CG1 - CG2) * M
Soit : (X + CG1) * m = (CG1 - CG2)*(M + m) et donc CG2 = CG1 - (X + CG1) * m/(M + m)
X + CG1 est la distance du lest au centre de gravité initial, donc L, et on a bien :
CG2 = CG1 - L * m / (M + m)
On trouve que CG2 est plus petit que CG1, ce qui veut dire que la distance de l'emplanture au centre de gravité a diminué et donc le centre de gravité a bien avancé.
On peut renverser la formule, pour déterminer quelle masse il faudrait ajouter à un endroit donné à l'avant de l'avion (généralement le plus en avant possible) pour avancer le centre de gravité d'une certaine distance. Il suffit de secouer un peu la formule et on trouve :
m = - M * (CG2 - CG1) / (L + (CG2 - CG1))
reprenons un exemple : modèle de 2kg400, CG initial à 10 cm de l'emplanture, on ajoute une masse de 100 grammes 20 cm en avant de l'emplanture, de combien avance la CG ?
On a alors CG1 = 10, X = 20, M = 2400 et m = 100 --> CG2 = CG1 - 30 * 100 / 2500 = CG2 - 1.2 cm.
CG2 = CG1 - 1.2 cm donc le centre de gravité a avancé de 1,2 cm suite à l'ajout de la masse.
Autre exemple, je souhaite avancer le centre de gravité de 2 cm avec une masse placée 20 cm en avant du bord d'attaque. La masse doit être égale à -2400 * (-20)/((200 + 100) + (-20)) = 171,4 grammes